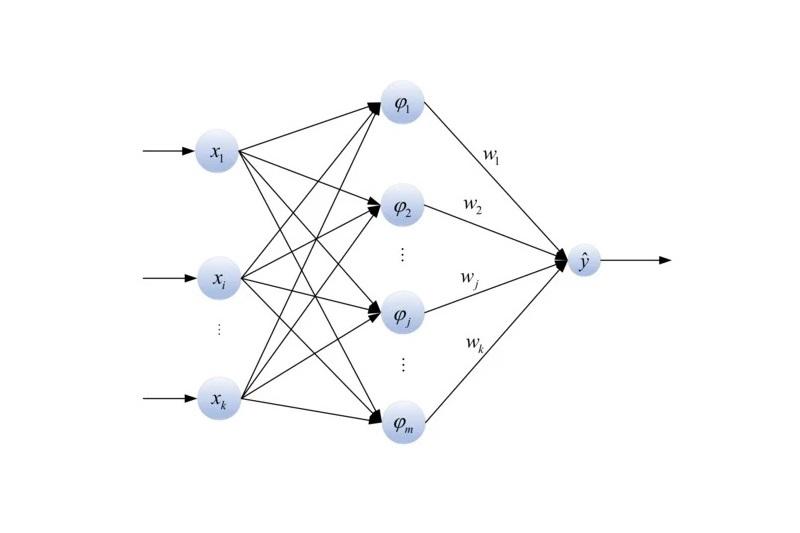
شبکه عصبی RBF چیست و چگونه در پایتون آن را پیاده‌سازی کنیم؟

شبکه عصبی RBF از سه لایه تشکیل شده است که شامل لایه ورودی، لایه پنهان (همچنین به عنوان لایه RBF شناخته می‌شود) و لایه خروجی است. هر نرون در لایه پنهان به عنوان یک تابع پایه شعاعی عمل می‌کند و ورودی‌ها را با استفاده از فاصله شعاعی بین ورودی و مرکزی که به آن نرون اختصاص داده شده است، تبدیل می‌کند. سپس، خروجی نرون‌های پنهان به لایه خروجی منتقل می‌شود که معمولا یک لایه خطی است. عملکرد شبکه RBF به این صورت است که مراکز نرون‌های پنهان به نحوی تنظیم می‌شوند که نزدیک‌ترین مرکز به ورودی مورد نظر بیشترین خروجی را تولید کند. در واقع، شبکه RBF قادر است به طور تقریبی تابع غیرخطی را تقریب بزند و بتواند الگوهای پیچیده را تشخیص دهد. برای آموزش شبکه RBF، معمولا از الگوریتم‌های یادگیری مانند الگوریتم Backpropagation استفاده می‌شود. شبکه RBF در موارد مختلفی مثل پیش‌بینی، تشخیص الگو، کنترل و تفکیک داده‌ها مورد استفاده قرار می‌گیرد.

شبکه عصبی شعای پایه چیست ؟

شبکه عصبی RBF نوعی خاص از شبکه‌های عصبی مصنوعی مبتنی بر فاصله است که شباهت بین داده‌ها را بر اساس فاصله می‌سنجد. این شبکه‌ها به دلیل سادگی و کارایی بالا در حل مسائل مختلف، از جمله پیش‌بینی، تقریب، دسته‌بندی و کنترل سیستم، مورد توجه بسیاری قرار گرفته‌اند. به طور کلی، شبکه عصبی RBF از سه لایه تشکیل شده که شامل لایه ورودی است که داده‌های ورودی را دریافت می‌کند. لایه پنهان که از تعدادی نرون تشکیل شده که هر کدام از یک تابع شعاعی پایه (RBF) برای محاسبه خروجی خود استفاده می‌کنند. توابع RBF معمولا توابع گوسی هستند و لایه خروجی که خروجی نهایی شبکه را محاسبه می‌کند.

شبکه عصبی شعاعی پایه از چه مولفه‌هایی ساخته شده است؟

شبکه عصبی شعاعی پایه (RBF) از مولفه‌های مختلفی به شرح زیر ساخته شده است.

• لایه ورودی (Input Layer): این لایه وظیفه دریافت ورودی‌ها را دارد. ورودی‌ها می‌توانند مقادیر عددی یا ویژگی‌هایی از داده‌ها باشند که برای آموزش یا تشخیص الگوها مورد استفاده قرار می‌گیرند.
• لایه پنهان (Hidden Layer): این لایه شامل نرون‌های پنهان است که به عنوان توابع پایه شعاعی عمل می‌کنند. هر نرون پنهان یک مرکز شعاعی دارد و با استفاده از فاصله شعاعی بین ورودی و مرکز، خروجی را تولید می‌کند. تعداد نرون‌های پنهان، تعداد مراکز شعاعی در شبکه را تعیین می‌کند.
• لایه خروجی (Output Layer): این لایه وظیفه ترکیب خروجی‌های نرون‌های پنهان و تولید خروجی نهایی را دارد. در برخی موارد، لایه خروجی می‌تواند لایه خطی باشد که خروجی‌های نرون‌های پنهان را به صورت خطی ترکیب می‌کند.
• مراکز شعاعی (Radial Centers): هر نرون پنهان یک مرکز شعاعی دارد. مراکز شعاعی معمولا با استفاده از روش‌های خوشه‌بندی مانند خوشه‌بندی k-means از داده‌های آموزش تعیین می‌شوند. این مراکز نشان دهنده مرکزهایی هستند که بهترین تطابق را با الگوهای ورودی دارند.
• تابع پایه شعاعی (Radial Basis Function): این تابع مسئول محاسبه فاصله شعاعی بین ورودی و مرکز شعاعی است. تابع گوسی معمولا به عنوان تابع پایه شعاعی استفاده می‌شود، که با استفاده از فاصله اقلیدسی بین ورودی و مرکز شعاعی، خروجی را تولید می‌کند.

مولفه‌های بالا در تعامل با یکدیگر شبکه عصبی RBF را تشکیل می‌دهند. با تعیین مراکز شعاعی و وزن‌دهی به هر نرون، شبکه قادر است به طور تقریبی تابع غیرخطی را تقریب بزند و الگوهای پیچیده را تشخیص دهد.

نحوه عملکرد شبکه عصبی RBF

عملکرد کلی شبکه شبکه عصب فوق به این صورت است که اولین مرحله آموزش نام دارد. در این مرحله، مراکز شعاعی (Radial Centers) برای نرون‌های پنهان (RBF Units) تعیین می‌شوند. این مراکز معمولا با استفاده از روش‌های خوشه‌بندی مانند خوشه‌بندی k-means از داده‌های آموزش تعیین می‌شوند. در ادامه وزن‌ها بین نرون‌های پنهان و لایه خروجی تعیین می‌شوند. در بیشتر موارد از الگوریتم Backpropagation برای آموزش شبکه استفاده می‌شود. هدف آموزش، تنظیم مراکز و وزن‌ها به گونه‌ای است که شبکه بتواند الگوهای ورودی را به درستی تشخیص دهد. مرحله بعد نوبت به تشخیص الگو می‌رسد. در این مرحله، وقتی ورودی به شبکه عصبی داده می‌شود، ابتدا فاصله شعاعی بین ورودی و مراکز شعاعی محاسبه می‌شود. این فاصله میزان تطابق ورودی با هر مرکز را نشان می‌دهد. سپس تابع پایه شعاعی از فاصله شعاعی محاسبه شده استفاده می‌کند تا خروجی هر نرون پنهان را تولید کند. این خروجی‌ها نشان دهنده میزان فعالیت نرون‌های پنهان است. در نهایت، خروجی نرون‌های پنهان با استفاده از وزن‌های مربوطه به لایه خروجی ترکیب می‌شوند و خروجی نهایی شبکه تولید می‌شود. در برخی موارد، لایه خروجی می‌تواند لایه خطی باشد که خروجی‌های نرون‌های پنهان را به صورت خطی ترکیب می‌کند.

مزیت اصلی شبکه RBF، توانایی آن در تقریب توابع غیرخطی و تشخیص الگوهای پیچیده است. با استفاده از مراکز شعاعی و وزن‌دهی به نرون‌ها، شبکه قادر است به طور تقریبی تابع مورد نظر را تقریب بزند. با توجه به توضیحاتی که ارائه کردیم باید بگوییم عملکرد شبکه فوق به شرح زیر است:

1.  داده‌های ورودی به لایه ورودی شبکه وارد می‌شوند.
2.  هر نرون در لایه پنهان، فاصله بین ورودی‌ها و مرکز خود را محاسبه می‌کند.
3.  نرون‌ها با استفاده از تابع RBF، خروجی خود را بر اساس این فاصله محاسبه می‌کنند.
4.  خروجی نرون‌ها در لایه پنهان به عنوان ورودی به لایه خروجی ارسال می‌شود.
5.  لایه خروجی با استفاده از یک تابع خطی، خروجی نهایی شبکه را محاسبه می‌کند.

مزایای شبکه عصبی RBF

شبکه عصبی RBF دارای مزایا و کاربردهای متعددی است. یکی از مزایای اصلی آن در مقایسه با سایر شبکه‌های عصبی، قدرت تقریب بالا در تقریب توابع غیرخطی است. شبکه RBF قادر است به طور تقریبی توابع پیچیده و الگوهای غیرخطی را با دقت بالا تقریب بزند. علاوه بر این، استفاده از توابع پایه شعاعی مانند تابع گوسی به شبکه اجازه می‌دهد تا به طور محدود واکنش نشان دهد و در نتیجه در مواجهه با داده‌های نویزی تحمل بهتری داشته باشد. علاوه بر آن، شبکه RBF دارای ساختار ساده‌تری نسبت به بسیاری از شبکه‌های عصبی است و در نتیجه آموزش و استفاده از آن نسبت به شبکه‌های عصبی پیچیده‌تر سریعتر و آسان‌تر است. این شبکه در حوزه‌های مختلفی مانند پیش‌بینی، تشخیص الگو، کنترل و تفکیک داده‌ها مورد استفاده قرار می‌گیرد. به طور کلی، شبکه عصبی RBF یک راه حل قوی و کارآمد برای مسائل پیچیده و غیرخطی است.

معایب شبکه عصبی RBF چیست؟

شبکه عصبی RBF دارای معایبی است که هنگام استفاده از آن باید مدنظر قرار داد. یکی از معایب اصلی آن نیاز به تعیین مراکز شعاعی است. این تعیین مراکز شعاعی معمولا با استفاده از الگوریتم خوشه‌بندی مانند k-means انجام می‌شود و نیاز به محاسبات گسترده دارد. همچنین، تعداد مراکز شعاعی باید به طور دقیق تعیین شود و این امر می‌تواند به یک مسئله پیچیده تبدیل شود. علاوه بر این، شبکه RBF در مواجهه با مسائل با ابعاد بالا ممکن است عملکرد نامناسبی داشته باشد، زیرا در ابعاد بالا، تعداد مراکز شعاعی زیاد شده و محاسبات پیچیده‌تری لازم است. همچنین، شبکه RBF نسبت به داده‌های نویزی حساس است و ممکن است در مواجهه با داده‌های نویزی عملکرد نامطلوبی داشته باشد. در نهایت، شبکه RBF کمتر قابل تفسیر است. به عبارت دیگر، نتایج و خروجی‌های آن را به راحتی نمی‌توان توضیح داد. این موضوع می‌تواند در برخی موارد که نیاز به تحلیل و تفسیر نتایج دارند مهم باشد.  با این وجود، با در نظر گرفتن مزایا و معایب شبکه عصبی RBF، انتخاب و استفاده مناسب از آن در پروژه‌های مناسب منجر به افزایش دقت و کارآیی می‌شود.

چگونه شبکه فوق را در پایتون پیاده‌سازی کنیم؟

اکنون اجازه دهید نحوه پیاده‌سازی عملی آن‌را در زبان برنامه‌نویسی پایتون مورد بررسی قرار دهیم. برای این منظور از کتابخانه scikit-learn استفاده می‌کنیم تا بتوانیم از شبکه RBF برای تقریب تابع سینوسی استفاده کنیم. ابتدا، باید کتابخانه scikit-learn را نصب کنید.

pip install scikit-learn

سپس، کد زیر را در یک فایل پایتون وارد کرده و اجرا کنید.

from sklearn.neural_network import RBFRegressor

import numpy as np

import matplotlib.pyplot as plt

# تولید داده‌های آموزشی

X_train = np.linspace(0, 2*np.pi, 100).reshape(-1, 1)

y_train = np.sin(X_train)

# ایجاد و آموزش شبکه RBF

rbf = RBFRegressor(n_centers=10, random_state=0)

rbf.fit(X_train, y_train)

# تست مدل با داده‌های تستی

X_test = np.linspace(0, 2*np.pi, 1000).reshape(-1, 1)

y_pred = rbf.predict(X_test)

# نمایش نتایج

plt.figure(figsize=(8, 6))

plt.scatter(X_train, y_train, color='blue', label='Training Data')

plt.plot(X_test, y_pred, color='red', label='RBF Prediction')

plt.xlabel('X')

plt.ylabel('y')

plt.title('RBF Regression')

plt.legend()

plt.show()

در این مثال، ابتدا داده‌های آموزشی برای تابع سینوسی تولید می‌شوند. سپس شبکه RBF با استفاده از کتابخانه scikit-learn ایجاد و با داده‌های آموزشی آموزش داده می‌شود. سپس با استفاده از داده‌های تستی، پیش‌بینی شده توسط شبکه RBF را رسم می‌کنیم. اجرای این کد، نموداری را نشان خواهد داد که نقاط آبی نمایش دهنده داده‌های آموزشی است و خط قرمز توسط شبکه RBF تولید شده است و تابع سینوسی را تقریب می‌دهد. این مثال نشان می‌دهد که چگونه می‌توانید شبکه RBF را در پایتون پیاده‌سازی کنید و از آن برای تقریب توابع غیرخطی استفاده کنید.

اکنون اجازه دهید کمی عملکرد قطعه کد بالا را بهبود دهیم تا بتواند با دقت بیشتری تابع سینوسی را تقریب بزند. یکی از راه‌های انجام این کار، افزایش تعداد مراکز شعاعی در شبکه RBF است. قطعه کد زیر این فرآیند را نشان می‌دهد.

from sklearn.neural_network import RBFRegressor

import numpy as np

import matplotlib.pyplot as plt

# تولید داده‌های آموزشی

X_train = np.linspace(0, 2*np.pi, 100).reshape(-1, 1)

y_train = np.sin(X_train)

# ایجاد و آموزش شبکه RBF با تعداد مراکز شعاعی بیشتر

rbf = RBFRegressor(n_centers=100, random_state=0)

rbf.fit(X_train, y_train)

# تست مدل با داده‌های تستی

X_test = np.linspace(0, 2*np.pi, 1000).reshape(-1, 1)

y_pred = rbf.predict(X_test)

# نمایش نتایج

plt.figure(figsize=(8, 6))

plt.scatter(X_train, y_train, color='blue', label='Training Data')

plt.plot(X_test, y_pred, color='red', label='RBF Prediction')

plt.xlabel('X')

plt.ylabel('y')

plt.title('RBF Regression')

plt.legend()

plt.show()

در قطعه کد بالا، تعداد مراکز شعاعی از 10 به 100 افزایش یافته است. این تغییر می‌تواند منجر به تقریب بهتر و دقیق‌تر تابع سینوسی توسط شبکه RBF شود. در نتیجه، خط قرمز حاصل از پیش‌بینی شبکه RBF به داده‌های واقعی نزدیک‌تر و هماهنگ‌تر خواهد بود.

یکی از ویژگی‌های مهمی که هنگام کار با شبکه‌های فوق باید به آن دقت کنید استفاده از یک معیار ارزیابی برای بررسی عملکرد مدل RBF است. یک معیار معمول برای ارزیابی عملکرد مدل رگرسیون استفاده از میانگین مربعات خطا (Mean Squared Error, MSE) است. فرآیند انجام این کار به شرح زیر است:

from sklearn.neural_network import RBFRegressor

from sklearn.metrics import mean_squared_error

import numpy as np

import matplotlib.pyplot as plt

# تولید داده‌های آموزشی

X_train = np.linspace(0, 2*np.pi, 100).reshape(-1, 1)

y_train = np.sin(X_train)

# ایجاد و آموزش شبکه RBF با تعداد مراکز شعاعی بیشتر

rbf = RBFRegressor(n_centers=100, random_state=0)

rbf.fit(X_train, y_train)

# تست مدل با داده‌های تستی

X_test = np.linspace(0, 2*np.pi, 1000).reshape(-1, 1)

y_pred = rbf.predict(X_test)

# محاسبه MSE

mse = mean_squared_error(np.sin(X_test), y_pred)

print(f"MSE: {mse}")

# نمایش نتایج

plt.figure(figsize=(8, 6))

plt.scatter(X_train, y_train, color='blue', label='Training Data')

plt.plot(X_test, y_pred, color='red', label='RBF Prediction')

plt.xlabel('X')

plt.ylabel('y')

plt.title('RBF Regression')

plt.legend()

plt.show()

در قطعه کد بالا پس از پیش‌بینی مقادیر با استفاده از شبکه RBF، میانگین مربعات خطا (MSE) بین مقادیر پیش‌بینی شده و مقادیر واقعی محاسبه می‌شود و در خروجی چاپ می‌شود. این معیار می‌تواند به شما اطلاعاتی درباره دقت مدل RBF در تقریب تابع سینوسی بدهد. اکنون قطعه کد بالا بالا قادر است شبکه RBF را با دقت بیشتری آموزش دهد و عملکرد آن را ارزیابی کند.