الگوریتم DBSCAN چیست و چگونه آن را پیاده سازی کنیم؟

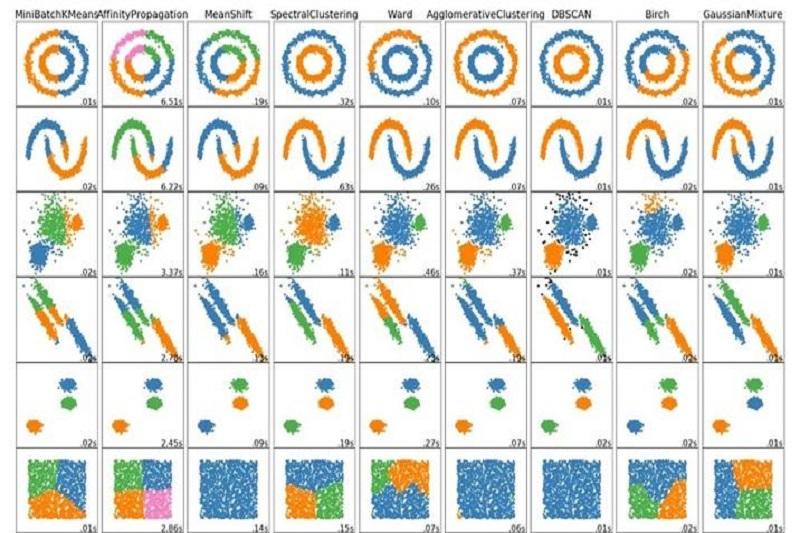
DBSCAN با تعیین یک نقطه شروع و تعیین آن به عنوان نقطه اصلی آغاز می‌شود. سپس تمام نقاط دیگر در گروهی که از این نقطه به آن‌ها دسترسی وجود دارد، بر اساس فاصله مشخصی (فاصله همسایگی) و آستانه چگالی مشخص شده، تعیین می‌شوند. این فرآیند برای نقاط دیگر در گروه تکرار می‌شود تا تمام نقاط مربوطه گردآوری شوند. نقاطی که به هیچ گروهی دسترسی ندارند، به عنوان نقاط نویز یا نقاط خراب شناخته می‌شوند. نقاط اصلی و نقاط مرزی در گروه‌های مختلف جمع‌آوری می‌شوند. یکی از ویژگی‌های DBSCAN قابلیت شناسایی خوشه‌های غیرمنظم و قابلیت مقابله با نویز و نقاط تنها است. می‌توان با استفاده از پارامترهایی مانند فاصله همسایگی و آستانه چگالی، الگوریتم را بر اساس نیازهای داده‌های خاص تنظیم کرد. بنابراین، DBSCAN امکان کشف خوشه‌های داده را با دقت و انعطاف بیشتری در داده‌های غیرمنظم و پیچیده فراهم می‌کند.

خوشه‌بندی چیست؟

خوشه‌بندی (Clustering) در علم داده‌ها، یک فرایند تحلیلی است که بر اساس شباهت و ارتباط بین داده‌ها، آن‌ها را در گروه‌های مشابه یا خوشه‌ها تقسیم می‌کند. هدف از خوشه‌بندی این است که داده‌های مشابه در یک خوشه قرار گیرند و داده‌های متفاوت در خوشه‌های مختلف قرار گیرند. در فرآیند خوشه‌بندی، داده‌ها بر اساس ویژگی‌های مشترک یا معیار‌های فاصله (مانند فاصله اقلیدسی یا فاصله منهتنی) مورد بررسی قرار می‌گیرند. الگوریتم‌های خوشه‌بندی سعی می‌کنند داده‌هایی که در نزدیکی یکدیگر قرار دارند، در یک خوشه قرار دهند و داده‌هایی که فاصله بزرگی از یکدیگر دارند، در خوشه‌های جداگانه قرار دهند.

خوشه‌بندی برای مجموعه‌ داده‌های بدون برچسب یا بدون دسته‌بندی قبلی استفاده می‌شود. این روش برای کشف الگوهای مخفی یا گروه‌بندی داده‌ها بسیار مفید است. به عنوان مثال، در علم کامپیوتر، خوشه‌بندی می‌تواند در تحلیل داده‌های مشتریان، تحلیل ترافیک، دسته‌بندی متن و بسیاری از برنامه‌های دیگر مورد استفاده قرار بگیرد. الگوریتم‌های مختلفی برای خوشه‌بندی وجود دارند، از جمله K-Means، DBSCAN، Hierarchical Clustering و Gaussian Mixture Models. انتخاب الگوریتم صحیح بسته به نوع داده و هدف خوشه‌بندی مورد نظر است.

خوشه‌بندی k-means

خوشه‌بندی K-Means یکی از رایج‌ترین الگوریتم‌های خوشه‌بندی است که بر اساس مرکز خوشه‌ها و فاصله بین نقاط مشترک در فضای ویژگی‌ها عمل می‌کند. الگوریتم K-Means با استفاده از مفهوم مرکز خوشه، نقاط را در خوشه‌های مشابه تقسیم می‌کند. کاربرد اصلی الگوریتم K-Means در تجزیه و تحلیل داده‌ها و خوشه‌بندی داده‌های بدون برچسب است. الگوریتم K-Means به این صورت عمل می‌کند که ابتدا فرآیند تعیین تعداد خوشه‌ها (K) انجام می‌شود. این تعداد می‌تواند براساس دانش اولیه یا با استفاده از روش‌های ارزیابی مانند روش Elbow تعیین شود. مرحله بعد نوبت به انتخاب نقاط اولیه به عنوان مراکز خوشه‌ها می‌رسد. نقاط اولیه برای مراکز خوشه‌ها به صورت تصادفی یا بر مبنای روش‌های دیگر انتخاب می‌شوند.

• محاسبه فاصله: فاصله بین هر نقطه داده و مراکز خوشه محاسبه می‌شود. می‌توان از فاصله اقلیدسی استفاده کرد.
• اختصاص خوشه: هر نقطه به نزدیک‌ترین مرکز خود اختصاص داده می‌شود و در آن خوشه قرار می‌گیرد.
• به‌روزرسانی مراکز خوشه: مراکز خوشه‌ها براساس نقاطی که به آن‌ها تعلق دارند، به‌روزرسانی می‌شوند. محاسبه مرکز جدید بر اساس میانگین مختصات نقاط موجود در هر خوشه انجام می‌شود.

این فرآیند ماهیت تکرارشونده دارد تا این که مراکز خوشه‌ها ثابت بمانند یا شرایط خاتمه برقرار شود. در نهایت، خوشه‌بندی نهایی بر اساس مراکز خوشه‌ها بدست می‌آید و می‌توانید داده‌ها را بر اساس این خوشه‌ها برچسب‌گذاری کنید.

الگوریتم DBSCAN چیست؟

همان‌گونه که اشاره کردیم الگوریتم DBSCAN یک روش خوشه‌بندی مبتنی بر چگالی است که نقاط داده‌ای را بر اساس تراکم و فاصله آنها از یکدیگر در خوشه‌های مختلف دسته‌بندی می‌کند. این الگوریتم به دو پارامتر اصلی نیاز دارد: شعاع همسایگی (ε) و حداقل تعداد نقاط در یک خوشه (MinPts).  در الگوریتم DBSCAN، نقاطی که در شعاع ε از یکدیگر قرار دارند، همسایه محسوب می‌شوند. اگر یک نقطه ε-همسایه‌های کافی (حداقل MinPts) داشته باشد، به عنوان نقطه "مرکزی" در نظر گرفته می‌شود. سپس، الگوریتم تمام نقاط همسایه "مرکزی" را به خوشه اضافه می‌کند. این فرآیند تا زمانی که هیچ نقطه "مرکزی" جدیدی یافت نشود، ادامه می‌یابد.  نقاطی که "مرکزی" نیستند و به هیچ نقطه "مرکزی" متصل نیستند، به عنوان "نویز" در نظر گرفته می‌شوند.  مزیت الگوریتم DBSCAN نسبت به روش‌های دیگر خوشه‌بندی مانند K-Means، عدم نیاز به تعیین تعداد خوشه‌ها از قبل است. همچنین، DBSCAN می‌تواند خوشه‌های با اشکال پیچیده را شناسایی کند و نقاط پرت (نویز) را به طور موثر تشخیص دهد.

عملکرد الگوریتم DBSCAN به چه صورتی است؟

الگوریتم DBSCAN قادر به تشخیص خوشه‌های با اشکال و اندازه‌های مختلف و همچنین شناسایی نقاط پرت است. به طور کلی،عملکرد الگوریتم DBSCAN به صورت زیر است:

ابتدا فرآیند تعیین پارامترها انجام می‌شود. از مهم‌ترین پارامترهای الگوریتم DBSCAN باید به اپسیلون Epsilon (ε) که شعاع همسایگی که نقاط در این شعاع به یکدیگر تعلق می‌گیرند را نشان می‌دهد و MinPts که تعداد حداقل نقاط مورد نیاز در شعاع همسایگی برای تشکیل یک خوشه را نشان می‌دهد، اشاره کرد.

مورد بعد انتخاب نقطه شروع است. یک نقطه را به صورت تصادفی انتخاب می‌کنیم و به عنوان نقطه شروع مشخص می‌کنیم. در مرحله بعد نوبت به تشخیص همسایگان می‌رسد. نقاط همسایه نسبت به نقطه شروع را با استفاده از شعاع همسایگی (ε) شناسایی می‌کنیم. اگر تعداد نقاط همسایه بیشتر از MinPts باشد، نقطه شروع به عنوان یک نقطه هسته تعریف می‌شود.

در ادامه با استفاده از روش گسترش خوشه، همسایگان همسایه را به خوشه اضافه می‌کنیم. به این صورت که برای هر نقطه هسته، تمام نقاط همسایه‌اش را به عنوان نقاط خوشه به خود اضافه می‌کنیم. سپس برای هر نقطه جدید اضافه شده به خوشه، همین روند را به صورت بازگشتی ادامه می‌دهیم تا دیگر نقاط هسته‌ای در شعاع همسایگی باقی نمانند. نقاطی که تعداد همسایه‌هایشان کمتر از MinPts است و همچنین به هیچ خوشه‌ای تعلق ندارند، به عنوان نقاط پرت شناخته می‌شوند. مراحل فوق به غیر از نقطه شروع را تکرار را برای نقاط باقیمانده تکرار می‌کنیم تا تمام نقاط پردازش شوند. در نهایت، خوشه‌های نهایی و نقاط پرت بر اساس نتیجه الگوریتم DBSCAN بدست می‌آوریم.

مزیت اصلی الگوریتم DBSCAN این است که می‌تواند خوشه‌های با شکل‌ها و اندازه متفاوت تشخیص دهد و نقاط پرت را شناسایی و جدا کند. الگوریتم DBSCAN قابلیت کشف خوشه‌هایی را دارد که چگالی نقاط در آن‌ها بال ااست و از خوشه‌های دیگر جدا هستند. همچنین، الگوریتم DBSCAN نقاط پرت را تشخیص می‌دهد که به هیچ خوشه‌ای تعلق ندارند و به تنهایی قرار دارند.

در حالت کلی، عملکرد الگوریتم DBSCAN به دو مرحله اصلی تقسیم می‌شود: تشخیص همسایگان و گسترش خوشه. این الگوریتم بر اساس مفهوم چگالی کار می‌کند، به این معنی که نقاطی که در شعاع همسایگی (ε) مشخص شده قرار دارند و تعداد همسایه‌هایشان بیشتر از MinPts است، به عنوان نقاط هسته شناخته می‌شوند و به خوشه اضافه می‌شوند. سپس خوشه با گسترش به نقاط همسایه ادامه می‌یابد. نقاطی که تعداد همسایه‌هایشان کمتر از MinPts است و به هیچ خوشه‌ای تعلق ندارند، به عنوان نقاط پرت شناسایی می‌شوند. در نهایت، الگوریتم DBSCAN خوشه‌های نهایی را به همراه نقاط پرت برمی‌گرداند که می‌توانند برای تجزیه و تحلیل داده‌ها و شناسایی الگوها و ساختارهای مختلف استفاده شوند.

چگونه الگوریتم DBSCAN را در پایتون پیاده سازی کنیم؟

برای پیاده‌سازی الگوریتم DBSCAN در پایتون، کتابخانه‌های مختلف در دسترس قرار دارند. یکی از روش‌های ساده برای پیاده‌سازی DBSCAN در پایتون استفاده از کتابخانه scikit-learn است. این کتابخانه شامل یک کلاس برای DBSCAN است که می‌توانید از آن استفاده کنید. در زیر مراحل پیاده‌سازی DBSCAN در پایتون با استفاده از scikit-learn نشان داده شده است.

1. نصب کتابخانه scikit-learn: قبل از هر چیز، اطمینان حاصل کنید که کتابخانه scikit-learn را نصب کرده‌اید. شما می‌توانید این کار را با استفاده از دستور زیر انجام دهید:

pip install scikit-learn

2. وارد کردن کتابخانه‌های مورد نیاز: برای پیاده‌سازی DBSCAN، نیاز به وارد کردن کتابخانه‌های زیر دارید:

from sklearn.cluster import DBSCAN

from sklearn.datasets import make_blobs

from sklearn.preprocessing import StandardScaler

import matplotlib.pyplot as plt

3. تولید داده‌های آزمایشی: برای تست الگوریتم، می‌توانید داده‌های آزمایشی تولید کنید. از تابع make_blobs در scikit-learn برای تولید خوشه‌های مصنوعی استفاده کنید. به عنوان مثال:

X, y = make_blobs(n_samples=100, centers=3, random_state=0, cluster_std=0.5)

4. مقیاس‌بندی داده‌ها: به طور معمول مقیاس‌بندی داده‌ها در DBSCAN عملکرد را بهبود می‌بخشد. برای این کار، از کلاس StandardScaler در scikit-learn استفاده کنید:

scaler = StandardScaler()

X_scaled = scaler.fit_transform(X)

5. اجرای الگوریتم DBSCAN: اکنون می‌توانید الگوریتم DBSCAN را اجرا کنید:

dbscan = DBSCAN(eps=0.3, min_samples=5)

dbscan.fit(X_scaled)

6. نتایج:  برای دسترسی به خوشه‌ها و نقاط پرت، می‌توانید از ویژگی‌های labels_ و core_sample_indices_ کلاس DBSCAN استفاده کنید:

labels = dbscan.labels_

core_samples_mask = np.zeros_like(labels, dtype=bool)

core_samples_mask[dbscan.core_sample_indices_] = True

7. نمایش نتایج: برای نمایش خوشه‌ها و نقاط پرت، می‌توانید از کتابخانه matplotlib استفاده کنید:

# نمایش خوشه‌ها

plt.scatter(X[:, 0], X[:, 1], c=labels)

plt.title('DBSCAN Clustering')

plt.xlabel('Feature 1')

plt.ylabel('Feature 2')

plt.show()

# نمایش نقاط پرت

plt.scatter(X[:, 0], X[:, 1], c=core_samples_mask)

plt.title('DBSCAN Outliers')

plt.xlabel('Feature 1')

plt.ylabel('Feature 2')

plt.show()

دستورات بالا مراحل کلی پیاده‌سازی الگوریتم DBSCAN در پایتون با استفاده از scikit-learn را نشان می‌دهد. البته، شما می‌توانید پارامترها و تنظیمات مختلفی را برای الگوریتم DBSCAN استفاده کنید  تا به عملکرد بهتری دست پیدا کنید.

مزایای الگوریتم DBSCAN

از مزایای DBSCAN باید به توانایی شناسایی خوشه‌های با اشکال و اندازه‌های مختلف اشاره کرد. DBSCAN قادر است خوشه‌هایی را که شکل و اندازه‌های متفاوتی دارند را شناسایی کند. این الگوریتم می‌تواند خوشه‌های با شکل‌های پیچیده مانند خوشه‌های نامنظم و خوشه‌های محلی را تشخیص دهد که الگوریتم‌هایی مبتنی بر مرکز خوشه نمی‌توانند این کار را به خوبی انجام دهند.

ویژگی کاربردی دیگر در ارتباط با توانایی شناسایی نقاط پرت است. DBSCAN قادر است نقاط پرت را شناسایی کند و آن‌ها را به عنوان خوشه‌های جداگانه مشخص کند. نقاط پرت معمولا نقاطی هستند که در هیچ خوشه‌ای قرار نمی‌گیرند و می‌توانند اطلاعات مهمی را درباره داده‌ها ارائه کنند. الگوریتم‌های دیگر معمولاً نقاط پرت را به عنوان نویز در نظر می‌گیرند و به درستی تشخیص نمی‌دهند.

مزیت شاخص دیگر الگوریتم فوق کارایی بالا است. DBSCAN از الگوریتم‌هایی است که می‌تواند با کمترین محاسبات، خوشه‌بندی دقیقی را انجام دهد. این الگوریتم به صورت یکپارچه و بدون نیاز به مرحله پیش‌پردازش می‌تواند با مجموعه ابتدایی داده‌ها عمل کند و نیازی به تعیین تعداد خوشه‌ها از قبل ندارد. این ویژگی باعث می‌شود که DBSCAN برای مجموعه‌های داده بزرگ و پیچیده بسیار مناسب باشد.

پایداری بالا در برابر نویزها. با توجه به مکانیزم کاری DBSCAN، نقاط پرت و نویز در صورتی که تعداد نقاط همسایه کم باشد، به عنوان نویز شناسایی می‌شوند و در خوشه‌بندی نهایی دخیل نمی‌شوند.

با توجه به این مزایا، DBSCAN به عنوان یک الگوریتم پرکاربرد و مفید در بسیاری از حوزه‌های مختلف از جمله تجزیه و تحلیل داده‌ها، تشخیص نقاط پرت، کاهش ابعاد و تجزیه پیچیدگی استفاده می‌شود. همچنین، DBSCAN می‌تواند به صورت موازی پیاده‌سازی شود و بنابراین برای کار با مجموعه‌های داده بزرگ مناسب است. با این حال، DBSCAN دارای چندین پارامتر است که باید به درستی تنظیم شوند تا عملکرد بهینه داشته باشد و در صورت عدم توجه به این نکته برخی را به وجود می‌آورند که اشتباه در انتخاب نقاط مرزی وابسته یکی از آن‌ها است.