اینترنت چگونه بسته‌های اطلاعاتی کاربران را از مبدا به مقصد انتقال می‌دهد؟

مسیریابی چیست؟

مسیریابی یونی‌کست (Unicast) در اینترنت، با تعداد زیادی روتر، میزبان و بر مبنای مسیریابی سلسله‌مراتبی و در چند مرحله با استفاده از الگوریتم‌های مسیریابی انجام می‌شود. در مسیریابی یونی‌کست، بسته از طریق جداول فوروارد، از مبدأ به مقصد و از یک هاپ به هاپ بعدی ارسال می‌شود. میزبان مبدا نیازی به ارسال جدول ندارد، زیرا بسته خود را به روتر پیش‌فرض در شبکه محلی تحویل می‌دهد. میزبان مقصد نیز نیازی به ارسال جدول ندارد، زیرا بسته را از روتر پیش‌فرض در شبکه محلی دریافت می‌کند. این حرف بدان معنا است که فقط روترهایی که شبکه‌ها را در اینترنت به یک‌دیگر متصل می‌کنند به جداول ارسال نیاز دارند. با توضیح فوق باید بگوییم که مسیریابی یک بسته از مبدأ به مقصد به‌معنای مسیریابی بسته از روتر مبدأ (روتر پیش‌فرض میزبان مبدا) به روتر مقصد (روتر متصل به شبکه مقصد) است. اگرچه یک بسته باید از مسیریاب‌های مبدأ و مقصد عبور کند، اما سوال این است که بسته باید از چه مسیریاب‌های دیگری عبور کند یا به عبارت دیگر، چند مسیر وجود دارد که یک بسته از مبدا تا مقصد طی می‌کند. 

برای یافتن بهترین مسیر، اینترنت را می‌توان به‌شکل گراف تصور کرد. برای مدل‌سازی اینترنت به‌عنوان یک گراف، می‌توانیم هر روتر را به‌عنوان یک گره و هر شبکه بین یک جفت روتر را به‌عنوان یک لبه در نظر بگیریم. اینترنت در واقع به‌عنوان یک گراف وزن‌دار مدل‌سازی می‌شود که در آن هر لبه هزینه‌ای دارد. اگر از گراف وزن‌دار برای نشان دادن یک منطقه جغرافیایی استفاده شود، گره‌ها می‌توانند شهرها و یال‌ها/لبه‌ها می‌توانند جاده‌هایی باشند که شهرها را به‌هم متصل می‌کنند. وزن‌ها، در این مورد، فواصل بین شهرها هستند. با این حال، در مسیریابی، هزینه یک لبه در پروتکل‌های مسیریابی مختلف متفاوت است. فرض کنید هزینه‌ای برای هر لبه وجود دارد. اگر هیچ لبه‌ای بین گره‌ها وجود نداشته باشد، هزینه بی‌نهایت است. شکل ۱ نشان می‌دهد که چگونه می‌توان مکانیزم عملکردی اینترنت را در قالب یک گراف ترسیم کرد. 

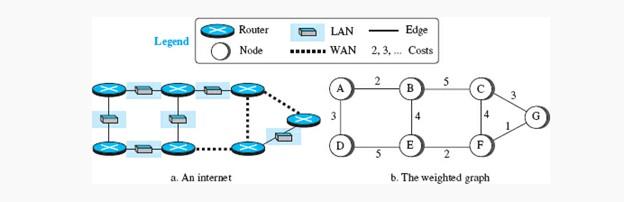
شکل 1

مسیریابی با کمترین هزینه

هنگامی که اینترنت را به‌عنوان یک گراف وزن‌دار مدل‌سازی می‌کنیم، یکی از راه‌های تفسیر بهترین مسیر از روتر مبدا به روتر مقصد محاسبه کمترین هزینه بین دو نقطه است. به‌عبارت دیگر، روتر مبدأ مسیری را برای رسیدن به روتر مقصد انتخاب می‌کند به‌گونه‌ای که هزینه کل مسیر کمترین هزینه را بین تمام مسیرهای ممکن داشته باشد. در شکل ۱، بهترین مسیر بین A و E، A-B-E با هزینه 6 است. این بدان معنا است که هر روتر باید مسیر کم‌هزینه بین خود و دیگر روترها را پیدا کند تا بتواند بسته‌ را در کوتاه‌ترین زمان برای مقصد ارسال کند. 

درختان کم‌هزینه (Least-Cost Trees)

اگر N روتر در اینترنت وجود داشته باشد، (N-1) بیان‌گر مسیرهای کم‌هزینه از هر روتر به هر روتر دیگر است. این بدان معنا است که ما به مسیرهای کم‌هزینه N×(N-1) نیاز داریم تا پهنای باند شبکه بیهوده هدر نرود. به‌طور مثال، اگر فقط 10 روتر در اینترنت داشته باشیم، به 90 مسیر کم‌هزینه نیاز داریم. یک راه بهتر برای مشاهده این مسیرها، ترکیب آن‌ها در قالب یک درخت کم‌هزینه است. درخت کم‌‌هزینه درختی با روتر منبع به‌عنوان ریشه است که همه گره‌ها تحت شبکه از آن بازدید می‌کنند و در آن مسیر بین ریشه و هر گره کوتاه‌ترین است. در این حالت، یک درخت، کوتاه‌ترین مسیر برای هر گره خواهد داشت. در دنیای واقعی، ما N درخت مسیر کم‌هزینه برای کل اینترنت داریم، با این‌حال، برخی از آن‌ها اهمیت بیشتری دارند. شکل ۲ هفت درخت کم‌هزینه مورد استفاده در اینترنت را نشان می‌دهد.

درخت‌های با کمترین ‌هزینه برای یک گراف وزن‌دار می‌توانند چند ویژگی مهم داشته باشند. 

مسیر کم‌هزینه از X به Y در درخت X معکوس مسیر کم‌هزینه از Y به X در درخت Y است. هزینه در هر دو جهت یکسان است. به‌عنوان مثال، در شکل ۲، مسیر A به F در درخت A به‌صورت (A → B → E → F) است، اما مسیر از F به A در درخت F به‌صورت (F → E → B → A) است. در هر مورد هزینه برابر با 8 است. 

به‌جای حرکت از X به Z با استفاده از درخت X، می‌توانیم از X به Y با استفاده از درخت X حرکت کنیم و از Y به Z با استفاده از درخت Y ادامه دهیم. به‌عنوان مثال، در شکل ۲، می‌توانیم از A به G در درخت A با استفاده از مسیر (A → B → E → F → G) حرکت کنیم. همچنین، می‌توانیم در درخت A از A به E برویم (A → B → E) و سپس در درخت E با استفاده از مسیر (E → F → G) کار را ادامه دهیم. ترکیب دو مسیر در حالت دوم همان مسیر مورد اول است. در نتیجه هزینه در مورد اول 9  و در مورد دوم نیز 9 (6 + 3) است.

شکل 2

الگوریتم‌های مسیریابی

درختان کم‌هزینه و جداول ارسالی یکی از مولفه‌های کلیدی هستند که پروتکل شبکه برای ارسال بسته‌ها با کمترین هزینه از آن‌ها استفاده می‌کند. الگوریتم‌های مسیریابی مولفه مهم دیگری هستند که نقش کلیدی در این زمینه دارد. تا به ‌امروزه، الگوریتم‌های مسیریابی مختلف طراحی شده‌اند. این الگوریتم‌ها در نحوه تفسیر کمترین هزینه و نحوه ایجاد درخت کم‌هزینه برای هر گره با یک‌دیگر متفاوت هستند. 

مسیریابی بردار فاصله

مسیریابی بردار فاصله (DV) سرنام Distance-Vector برای یافتن بهترین مسیر استفاده می‌شود. در مسیریابی بردار فاصله، اولین چیزی که هر گره ایجاد می‌کند درخت کم‌هزینه خود با اطلاعات اولیه است که در مورد همسایگان نزدیک دارد. درخت‌های ناقص بین همسایگان ارسال و دریافت می‌شوند تا به‌تدریج به درختان کامل و کامل‌تر قابل استفاده در اینترنت تبدیل شوند. می‌توان گفت در مسیریابی بردار فاصله، یک روتر به‌طور مداوم به همه همسایگان خود درباره آن‌چه در مورد کل اینترنت می‌داند اطلاع‌رسانی می‌کند، هرچند این آگاهی‌رسانی ناقص باشد. قبل از این‌که نشان دهیم چگونه درختان ناقص کم‌هزینه را می‌توان ترکیب کرد تا درخت‌های کامل ایجاد شوند، باید به دو مبحث مهم معادله بلمن-فورد و مفهوم بردارهای فاصله بپردازیم.

معادله بلمن-فورد

در قلب مسیریابی بردار فاصله، معادله معروف بلمن-فورد قرار دارد. این معادله برای یافتن کمترین هزینه (کوتاه‌ترین فاصله) بین گره مبدا x، گره مقصد y و از طریق برخی از گره‌های واسطه (a, b, c,…) استفاده می‌شود تا هزینه‌ بین منبع و گره‌های واسطه محاسبه شود و کمترین هزینه بین گره‌های واسطه و مقصد داده به‌دست آید. در فرمول زیر Dxy کمترین فاصله را نشان می‌دهد. 

Dxy=min{(cxa+Day), (cxb + Dby), (cxc + Dcy), …}

در مسیریابی بردار فاصله، در نظر داریم حداقل هزینه موجود را با کمترین هزینه از طریق یک گره واسطه، مانند z، به‌روزرسانی کنیم تا ببینیم گره دوم کوتاه‌تر است یا خیر. در این حالت، معادله را می‌توان به‌شکل ساده‌تر زیر نوشت: 

Dxy=min{Dxy, (cxz+Dzy)}

نمای گرافیکی معادله بلمن-فورد در شکل ۳ نشان داده شده است. 

معادله بلمن-فورد به ما اجازه می‌دهد از مسیرهای کم‌هزینه قبلی، یک مسیر کم‌هزینه جدید بسازیم. در شکل ۳، می‌توانیم (a → y)، (b → y)  و (c → y) را به‌عنوان مسیرهای کم‌هزینه قبلی و (x → y) را به‌عنوان مسیر کم‌هزینه جدید در نظر بگیریم و معادله جدید را به‌عنوان سازنده یک درخت کم‌هزینه جدید از درخت‌های کم‌هزینه قبلی پیاده‌سازی کنیم. به عبارت دیگر، استفاده از این معادله در مسیریابی بردار فاصله گواه این مسئله است که در این روش از درختان کم‌هزینه برای یافتن بهترین مسیر استفاده می‌شود. 

شکل 3

بردارهای فاصله (Distance Vectors)

بردار فاصله، پایه و اساس مسیریابی بردار فاصله را شکل می‌دهد. درخت کم‌هزینه ترکیبی از مسیرهای کم‌هزینه از ریشه درخت به تمام مقصدها است. این مسیرها به‌صورت گرافیکی به یک‌دیگر متصل می‌شوند تا درخت را پدید آورند. مسیریابی بردار فاصله این مسیرها را باز می‌کند تا بتواند یک بردار فاصله و یک آرایه یک‌ بعدی برای نشان دادن درخت تعریف کند. 

اکنون می‌دانیم یک بردار فاصله می‌تواند مسیرهای کم‌هزینه در یک درخت کم‌هزینه را نشان دهد، اما چگونه هر گره در اینترنت بردار مربوطه را ایجاد می‌کند. هر گره در اینترنت، هنگامی که وارد مرحله عملیاتی می‌شود، یک بردار فاصله بسیار ابتدایی با حداقل اطلاعاتی که از گره همسایه خود به‌دست آورده ایجاد می‌کند. گره، پیام‌های خوشامدگویی را برای رابط‌های مجاور ارسال می‌کند تا هویت همسایگان و فاصله بین خود و هر همسایه را کشف کند. در ادامه، با درج فواصل کشف‌شده در سلول‌های مربوطه، یک بردار فاصله ساده می‌سازد و مقدار سلول‌های دیگر را بی‌نهایت در نظر می‌گیرد. آیا این بردارهای فاصله نشان‌دهنده مسیرهای کم‌هزینه هستند؟ در ابتدای کار این‌گونه به‌نظر می‌رسد. در ابتدای کار که تنها فاصله بین دو گره را می‌دانیم، مسیر اولیه به‌عنوان کم‌هزینه‌ترین مسیر در نظر گرفته می‌شود، اما به‌تدریج که اطلاعات کامل می‌شوند، شناخت دقیق‌تری در ارتباط با کم‌هزینه‌ترین مسیر به‌دست می‌آید. شکل ۴ بردارهای فاصله‌ای را که اینترنت از آن‌ها استفاده می‌کند نشان می‌دهد. دقت کنید این بردارها به‌صورت غیرهمزمان ساخته می‌شوند. 

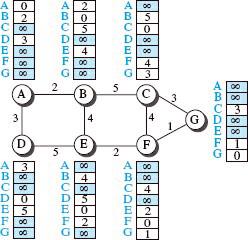
شکل 4

این بردارهای ابتدایی نمی‌توانند به شبکه اینترنت برای ارسال بهینه یک بسته کمک کنند. در شکل ۴، گره A تصور می‌کند که به گره G متصل نیست، زیرا سلول مربوطه کمترین هزینه بی‌نهایت را نشان می‌دهد. برای بهبود عملکرد این بردارها، گره‌ها در اینترنت باید با تبادل اطلاعات به یک‌دیگر کمک کنند. پس از این‌که هر گره بردار خود را ایجاد کرد، یک کپی از بردار برای همه همسایگان نزدیک ارسال می‌کند. پس از این‌که یک گره بردار فاصله را از همسایه دریافت کرد، بردار فاصله خود را با استفاده از معادله بلمن-فورد (مورد دوم) به‌روز می‌کند. 

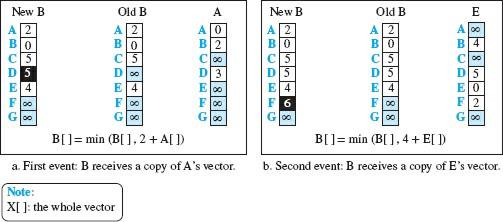
شکل 5

در شکل ۵، دو رویداد غیرهمزمان را مشاهده می‌کنیم که یکی پس از دیگری با فاصله زمانی اتفاق می‌افتند. در رویداد اول، گره A بردار خود را برای گره B ارسال می‌کند. گره B بردار خود را با استفاده از هزینه cBA = 2 به‌روز می‌کند. در رویداد دوم، گره E بردار خود را برای گره B ارسال می‌کند و گره B بردار خود را با استفاده از cEA = 4 به‌روز می‌کند.  بعد از اولین رویداد، بردار گره B کمی بهبود پیدا می‌کند و حداقل هزینه آن برای گره D از بی‌نهایت به 5 (از طریق گره A) تغییر می‌کند. بعد از رویداد دوم، بردار گره B باز هم بهبود پیدا می‌کند و حداقل هزینه آن برای گره F از بی‌نهایت به 6 (از طریق گره E) تغییر می‌کند. تبادل بردارها در نهایت عملکرد شبکه را تثبیت می‌کند و به گره‌ها اجازه می‌دهد حداقل هزینه بین خود و هر گره دیگر را بیابند. به خاطر داشته باشید که پس از به‌روز‌رسانی یک گره، بلافاصله بردار به‌روزشده برای همه همسایگان ارسال می‌شود. حتا اگر همسایگان بردار قبلی را داشته باشند، بازهم نسخه به‌روزشده را دریافت می‌کنند. شبه‌کد ساده‌شده برای الگوریتم مسیریابی بردار فاصله در شکل ۶ نشان داده شده است. الگوریتم مذکور توسط هر گره به‌طور مستقل و غیرهمزمان اجرا می‌شود.

شکل 6

خطوط 4 تا 11 بردار گره را مقداردهی اولیه می‌کنند. خطوط 14 تا 23 نشان می‌دهند که چگونه می‌توان بردار فعلی را پس از دریافت بردار جدید از همسایه به‌روزسانی کرد. حلقه for خطوط 17 تا 20 اجازه می‌دهد تمام ورودی‌ها (سلول‌ها) در بردار پس از دریافت بردار جدید به‌روز شوند. توجه داشته باشید که گره، بردار خود را در خط 12 پس از مقداردهی اولیه و در خط 22 پس از به‌روزرسانی ارسال می‌کند.