بخش اول: آشنایی با مهمترین الگوریتمهای بازیابی اطلاعات
الگوریتم B*
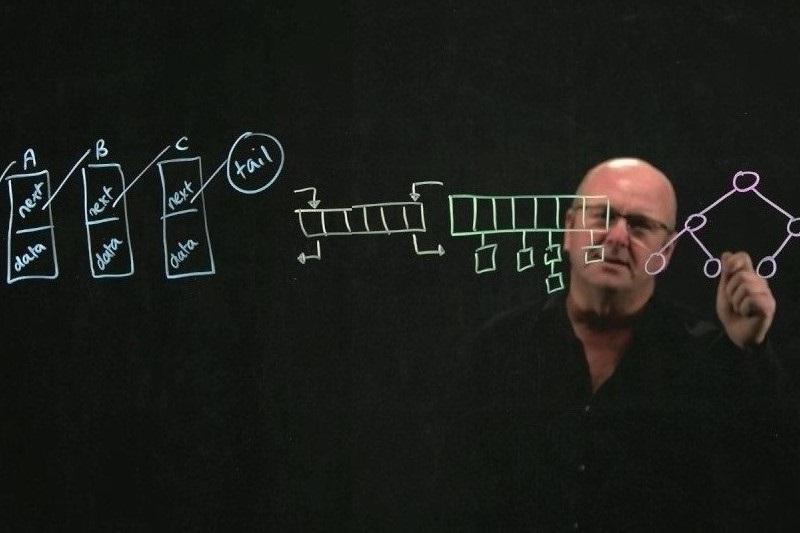
درخت بیاستار، یک نوع خاص از درخت بیپلاس است. درختهای بی، بیاستار و بیپلاس در پایگاه دادهها و سیستم فایلها کاربرد زیادی دارند. الگوریتم بی استار(B*) یک الگوریتم جستجوی ابتدا بهترین در گراف است. در این روش، کمهزینهترین مسیر از یک گره به گره هدف در گراف محاسبه میشود. این الگوریتم اولین بار در سال ۱۹۷۹ توسط هانس برلینر ارائه شد که با الگوریتم الگوریتم جستجوی A* مرتبط است. درختهای بی، بی استار و بی پلاس در پایگاه دادهها و سیستم فایلها کاربرد زیادی دارند و در داده ساختارها و پایگاهدادهها به منظور شاخص بندی استفاده میشوند. یک درخت بی یا بیتری (B-tree) دادهساختاری درختی است که دادهها را به صورت مرتبشده نگه میدارد و جستجو، درج و حذف را در زمان لگاریتمی میسر میسازد. بر خلاف درختهای جستجوی دودویی متوازن (Balanced binary search tree)، این دادهساختار برای سیستمهایی که بلاکهای عظیم اطلاعات را خوانده و مینویسند بهینهسازی شدهاست. این دادهساختار معمولاً در پایگاهدادهها و سیستم پرونده استفاده میشود.
در درخت بی دادهها میتوانند در برگها یا گرههای میانی ذخیره شوند. اما در درخت بیپلاس، تمام دادهها در برگها ذخیره میشوند و یک گره توانایی نگهداری چند داده به جای یک داده هم دارد. درخت B* نوع خاصی از درخت +B است که حداقل دو سوم از ظرفیت هر گره تکمیل باشد.

ارزیابی با درختهای مشابه
تفاوت اساسی که بین درخت بیاستار و بی پلاس وجود دارد این است که در درخت بیپلاس، هر گره وقتی دارای یک گره فرزند خواهد شد که کامل باشد. دادهها در یک گره درخت بی پلاس، نصف ظرفیت آن هستند؛ که این مقدار در درخت بیاستار، دو سوم ظرفیت آن است. پس درخت بیاستار در مقایسه با بیپلاس متراکم تر است. از مهمترین تفاوتهای اصلی یک درخت دودویی و درخت بی استار میتوان به وجود دادههای چند گانه در یک گره در درخت به استار به جای یک داده در درخت دودویی، در درخت بیاستار هر گره در کنار یک لیست از دادههای مرتب شده، یک اشاره گر به گره بعدی هم دارد و بی توازن بودن درخت بیاستار اشاره کرد.
در سایر الگوریتمهای جستجو، برای انجام جستجوهای تکراری، یک راه طبیعی برای پایان جستجو وجود ندارد. همچنین با در نظر گرفتن محدودیتهای مختلف این نکته که کدام عنصر باید ریشه واقع شود، چیز ثابتی نیست. برای غلبه بر این مشکلات از الگوریتم جستجوی بی استار استفاده میکنیم. دو نکته مهم زیر میتواند الگوریتم B* را به عنوان یک الگوریتم ابندا-بهترین ساده متمایز سازد:
اول آنکه الگوریتم B* ، فرایند پشتیبانی را اجرا میکند هر گاه به جایی برسد که مقدار آن برای مسئله ما کافی است. در حالی که سایر الگوریتمهای ابتدا-بهترین، تا مقدار نهایی را نیابند فرایند پشتیبانی را اجرا نمیکنند. یک نکته ظریف اینجا وجود دارد و آن این است که بی معنی ایت اگر حرکت را از یک گره ادامه بدهیم در حالی که گره موجود حاوی مقداری است که مناسب انتخاب شدن است. در حالی که سایر روشهای ابتدا-بهترین این را نمیفهمند.
دوم آنکه الگوریتم میتواند یکی از دو روش را فقط وقتی روی ریشه است انتخاب کند. این باعث میشود ادامه الگوریتم در مسیری حرکت کند که کم هزینهترین حرکتها مشخص شود.

الگوریتم اکس
الگوریتم اکس به رویکرد واضح سعی و خطا برای یافتن تمام پاسخهای ممکن برای مسئله پوشش دقیق، بکار بردهاست. از نظر فنی الگوریتم اکس یک الگوریتم بازگشتی، غیر قطعی، عمق-اول با پس گرد است. در حالی که الگوریتم اکس بهطور کلی به عنوان یک توضیح موجز برای بیان راه حل مسئله پوشش دقیق مفید است، ممکن است منظور راه حل کنوث در ارائه آن صرفاً برای نشان دادن روش ابزار پیوندهای رقصنده با استفاده از یک پیادهسازی کارای آن تحت عنوان DLX باشد.
الگوریتم MTD-F
MTD-F که در واقع خلاصه شده ی (MTD(f,n میباشد (درایور تست با حافظه ی اضافی با گره n و مقدار f) الگوریتمی برای جستجوی minimax است که میتوان به عنوان جایگزینی برای الگوریتم هرس آلفا و بتا از آن استفاده کرد.
MTD-F بهطور کارآمد و موثری، جستجوهایی که فقط zero-window و آلفا و بتا باشند را با کران خوبی انجام میدهد (با بتای متغیر). در نگااسکاتآلفا بتا با یک فضای جستجو نمایان میشود. در (AlphaBeta(root, -INFINITY, +INFINITY, depth)) مقدار خروجی بین آلفا و بتا میباشد. در الگوریتم فوق آلفا بتا برای یافتم کران بالا یا کران پایین برای مقدار بیشینه، اشتباه میکند. zero-window برای بیشتر بودن راههای میان بر و مقدارهای بازگشتی کمتر، استفاده میشود. برای یافتم مقدار بیشینه MTD-F، آلفا بتا را چندین بار صدا میزند تا در نهایت مقدار دقیق و نهایی را پیدا کند. جدول تقدم و تاخر جستجوهای قدیمی را بر می گرداند و همچنین جستجوهای جدید را برای کاهش رجوع مجدد به جستجو ذخیره میکند. ثابت شده که پیادهسازی این الگوریتم از سایر الگوریتمهای جستجوی دیگر (مانند نگا اسکات)، مخصوصاً برای بازیهایی مانند شطرنج کارآمد تر است. اما در عمل این الگوریتم ایراداتی نیز دارد مانند اتکای بیش از حد به جدول تقدم و تاخر، بی ثباتی جستجو، و بسیاری مورد دیگر. بنابراین غالب موتورهای بازی شطرنج، همچنان از نگا اسکاتی استفاده میکنند که به نظر بسیاری از برنامه نویسهای شطرنج بهترین الگوریتم برای شطرنج است.

الگوریتم A*
در علوم کامپیوتر، الگوریتم A* یک الگوریتم مسیریابی است که برای پیمایش و یافتن مسیر در گراف استفاده میشود. به علت کامل بودن، بهینه بودن (یافتن جواب بهینه) و سرعت مناسب این الگوریتم، استفاده گستردهای از آن میشود. مشکل اصلی این الگوریتم استفاده زیاد از حافظه است که باعث میشود در بسیاری از مسائل عملی ضعیفتر از سایر الگوریتمها عمل کند. این الگوریتم در واقع تعمیمی از الگوریتم دیکسترا است که با استفاده از روشهای فرا ابتکاری عملکرد بهتری در زمینه جستجو بدست آوردهاست. A* یک جستجوی آگاهانه یا یک جستجوی ابتدا بهترین است که یعنی از یک گره مشخص (گره شروع) جستجو را آغاز میکند و هدفش پیدا کردن یک مسیر به گره نهایی یا هدف است که کمترین هزینه را دارد. این روش با ترکیب g/n هزینه رسیدن به گره n و h(n) هیوریستیک یا تخمین هزینه رسیدن از گره n تا هدف گرهها را ارزیابی میکند:
F(n)=G(n)+ h(n)
از آنجایی که g(n) هزینه مسیر از گره شروع به گره n و h(n) هزینه تخمینی ارزانترین مسیر از n به هدف است، داریم:
F(n)=n هزینه برآورد ارزان ترین راه حل از طریق
بنابراین اگر به دنبال ارزانترین راه حل هستیم، اولین کار معقول امتحان گرهای است که کمترین مقدارh(n) + g(n) را داراست. مشخص میشود که این راهبرد کاملاً معقولانهاست. اگر تابع آروین h(n) قابل قبول و جستجو درختی باشد الگوریتم بهینه است. اما اگر جستجوی گراف باشد علاوه برای قابل قبول بودن لازم است تا یکپارچه نیز باشد.
اگر A* همراه با الگوریتم جستجوی درخت استفاده شود، آنگاه تحلیل بهینگی آن بسیار ساده و سر راست میشود. A* بهینهاست اگر h(n) یک آروین قابل قبول باشد. یعنی h(n) هرگز هزینه رسیدن به هدف را بیش از اندازه واقعی برآورد نکند. این آروینها ذاتاً بهینه هستند زیرا آنها فکر میکنند که هزینه راه حل مسئله کمتر از مقدار واقعی آن است. از آنجا که g(n) هزینه رسیدن به n را بهطور دقیق نشان میدهد، میتوان بلافاصله نتیجه گرفت که f(n) هرگز هزینه واقعی راه حلی که از n میگذرد را اضافه برآورد نمیکند. پیاده سازی معمول A* از یک صف اولویتدار استفاده میکند تا گره های دارای کمترین هزینه براورد شده را در هر مرحله برای باز کردن انتخاب کند. در هر مرحله، گره با کمترین f از صف حذف میشود، سپس تابع f همسایههای آن گره به روز رسانی میشود و در نهایت همسایهها به صف اضافه میشوند. جستجو زمانی به پایان میرسد که یا مسیری از گره شروع به هدف یافت نمیشود، به عبارت دیگر صف خالی میشود و دیگری گرهای برای باز کردن وجود ندارد. یا به گره هدف میرسد که در این صورت مقدار f همان کمترین هزینه است برای رسیدن به گره هدف، زیرا تابع h در هدف به علت قابل قبول بودن 0 است.
کارهای زیادی برای بهبود عملکرد این الگوریتم میتوان انجام داد. یکی از این کارها نحوهی انتخاب گرههای با هزینههای یکسان از صف اولویت است. اگر در شرایط تساوی f چند گره، پیادهسازی به نحوی باشد که آخرین گره ورودی اولین گره خروجی باشد (LIFO)، الگوریتم مشابه جستجو عمق اول عمل میکند و از جستجوی مسیرهای بهینه با هزینه یکسان جلوگیری میکند. اگر به جز هزینه کمینه خود مسیر هم مورد سوال باشد، لازم است که در هر گره یک اشارهگر به پدر آن گره وجود داشته باشد که با پایان جستجو بتوان مسیر را با دنبال کردن اشارهگرها یافت. اما در این حالت باید از حضور چند نمونه از یک گره در صف جلوگیری شود. یک روش این است که اگر گره خواست به صف اضافه شود ولی در صف حضور داشت، به جای اضافهکردن مجدد آن، اشارهگر پدر و هزینهی گره موجود در صف، بروزرسانی گردد. این کار توسط صف هایی که بر اساس هرم دودویی ساخته شده اند به تنهایی ممکن نیست ولی میتوان با کمک گرفتن از جدول درهمسازی برای ذخیره مکان گره در هرم بروزرسانی را انجام داد. همچنین روشهای دیگری مثل استفاده از هرم فیبوناچی برای ساخت صف اولویت نیز قابل استفاده هستند.
الگوریتم جستجوی رشته بویر
الگوریتم جستجوی رشته بویر مور یکی از الگوریتمهای مؤثر جستجوی رشته است که توسط رابرت بویر و جی استراسر مور در سال 1977 منتشر شدهاست. این الگوریتم رشته االگو را پیش پردازش میکند اما رشته متن را پیش پردازش نمیکند. این الگوریتم زمانی مناسب است که رشته الگو بسیار کوتاهتر از رشته متن باشد. این الگوریتم با استفاده از اطلاعاتی که از پیش پردازش الگو به دست میآورد بعضی از قسمتهای متن را بررسی نمیکند. بنابراین نسبت به بسیاری از الگوریتمهای دیگر ضریب ثابت پایین تری دارد. ایده اصلی الگوریتم این است که به جا اینکه سر الگو را با متن مقایسه کند انتهای الگو را با متن مقایسه میکند.
الگوریتم بویر مور به دنبال تطابقهای رشته P در رشته T به وسیله مقایسه کاراکتر در هم طرازیهای متفاوت می گردد. به جای جستجوی خام همه هم طرازیهای متفاوت (که تعداد آنها n - m + 1 است) ، بویر مور از اطلاعات پیش پردازش P استفاده میکند تا جای که امکان دارد هم طرازیهای کمتری را بررسی کند. راه معمول جستجوی یک متن مقایسه کاراکترهای آن با اولین کاراکتر الگو است. هنگامی که دو کاراکتر یکسان بودند مابقی کاراکترهای متن با کاراکترهای الگو مقایسه میشوند. اگر تطابقی وجود نداشت دوباره متن ، کاراکتر به کاراکتر برای پیدا کردن تطابق بررسی میشود. بنابراین بیشتر کاراکترهای متن باید بررسی شود. نکته کلیدی این الگوریتم این است که با مقایسه انتهای الگو با کاراکترهای متن بسیاری از کاراکترهای متن را بررسی نمیکند. چراکه اگر دو کاراکتر یکسان نباشند نیاز نیست تا تمام کاراکترهای دیگر را عقب گرد بررسی کنیم. نکته جالب اینجاست که اگر این کاراکتر با هیچکدام از کاراکترهای الگو یکسان نباشد ، کاراکتر بعدی که در متن نیاز به بررسی در متن دارد ؛ n (طول الگو) موقعیت جلوتر است. اگر این کاراکتر در الگو وجود داشت یک انتقال جزئی صورت میگیرد تا این دو کاراکتر زیر هم قرار گیرند. این انتقالها باعث میشود که تعداد کاراکترهایی که باید بررسی شوند کاهش یابد. بهطور دقیقتر، الگوریتم با هم طرازی k = n شروع میشود؛ بنابراین شروع P با شروع T هم طراز میشود. سپس کاراکترهای P و T از موقعیت n ام به صورت عقبگرد با هم مقایسه میشوند. مقایسه ادامه می یابد تا هنگامی که یا به ابتدای p برسیم(یک تطابق پیدا کردیم) ؛ یا عدم تطابق مشاهده شود که در این صورت با استفاده از قوانین زیر الگو را بیشترین مقدار ممکن انتقال می دهیم و مقایسهها در هم طرازی جدید انجام میشود. این روند تا جایی ادامه می یابد که که الگو به مکانی بعد از انتهای T انتقال یابد که به این معناست که تطابق جدیدی وجود ندارد.انتقالها با استفاده از جداولی که از پیش پردازش P به دست میآید در (1)O اجرا میشود.
الگوریتم Hilltop
الگوریتم تپه Hilltop الگوریتمی است که برای پیدا کردن اسناد مربوط به یک کلمه کلیدی خاص استفاده میشود. وقتی که یک پرسش یا کلمهکلیدی را در موتورهای جستجوی گوگل وارد میکنید، الگوریتم Hilltop برای پیدا کردن کلمات کلیدی مرتبط و حاوی اطلاعاتی مفیدتر به گوگل کمک میکند. این الگوریتم بر روی یک شاخص خاص از اسنادهای متخصص به اجرا در میآید. اینها صفحاتی پیرامون یک موضوع خاص هستند و لینکهایی را به صفحات غیر وابسته دیگری مرتبط با آن موضوع دارند. نتایج بر اساس یک تطابق رتبهبندی میشوند. در واقع این الگوریتم بین صفحات «متخصص» و «معتبر» ارتباط برقرار میکند: یک صفحه تخصصی، صفحهای است که لینکهای بسیاری از اسناد دیگر و البته مرتبط، به آن پیوند داده میشوند. از طرفی یک صفحه معتبر و مقتدر نیز صفحهای است که در مورد یک موضوع خاص صحبت میکند و به بسیاری از صفحات غیر وابستهای که بدان موضوع مرتبط هستند لینک میدهد، در واقع به صورت یک مرجع شناخته میشود. اگر یک وبسایت به صفحات متخصص لینک دهد، یک مقتدر یا معتبر یا همان مرجع خواهد شد. در تئوری، گوگل در ابتدا صفحات متخصص را پیدا میکند و پس از آن صفحاتی که به آن لینک دادهاند به رتبه خوبی خواهند رسید، به این معنی که در نمایش نتایج موتورهای جستجو اولویت با صفحه متخصص و پس از آن صفحات لینک داده شدهاست. صفحات در سایتهایی مانند یاهو، DMOZ یا سایتهای دانشگاهی و کتابخانهای معمولاً صفحات متخصص در نظر گرفته میشوند.
ماهنامه شبکه را از کجا تهیه کنیم؟
ماهنامه شبکه را میتوانید از کتابخانههای عمومی سراسر کشور و نیز از دکههای روزنامهفروشی تهیه نمائید.
ثبت اشتراک نسخه کاغذی ماهنامه شبکه
ثبت اشتراک نسخه آنلاین
کتاب الکترونیک +Network راهنمای شبکهها
- برای دانلود تنها کتاب کامل ترجمه فارسی +Network اینجا کلیک کنید.
کتاب الکترونیک دوره مقدماتی آموزش پایتون
- اگر قصد یادگیری برنامهنویسی را دارید ولی هیچ پیشزمینهای ندارید اینجا کلیک کنید.
























نظر شما چیست؟