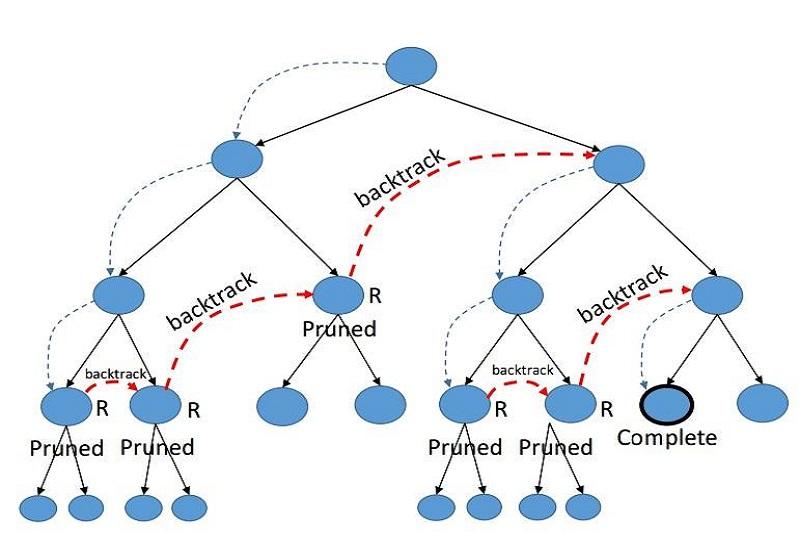
فرض کنید که شما با یک مسئله مواجه هستید که برای حل آن، باید تصمیمهای زنجیرهای را اتخاذ کنید. هر تصمیم میتواند به چندین تصمیم دیگر منجر شود و هر تصمیم همراه با یک مجموعه شرطی است که بررسی میکند که آیا این تصمیم به پاسخ نهایی ما منجر میشود یا خیر.
وقتی از الگوریتم Backtracking استفاده میکنید، ابتدا یک تصمیم را اتخاذ میکنید و شروع به اجرای شرایط مربوطه میکنید. در هر مرحله، اگر شروط زنجیرهای برقرار نباشند، به مرحله قبلی برمیگردید و تصمیم دیگری را امتحان میکنید. اگر تمام تصمیمهای ممکن را بررسی کرده و به پاسخ نهایی نرسیدید، به مرحله قبلی برمیگردید و تصمیمهای دیگری را امتحان میکنید. این فرایند تا زمانی ادامه مییابد که به یک پاسخ نهایی برسید یا تمام تصمیمها را امتحان کنید و به این نتیجه برسید که پاسخ موجود نیست.
نکات مهمی که باید در مورد الگوریتم عقبگرد بدانید
- الگوریتم Backtracking معمولاً با استفاده از یک تابع بازگشتی پیاده سازی میشود. این تابع با انتخاب یک تصمیم و بررسی شرایط زنجیرهای، خود را به صورت بازگشتی فراخوانی میکند تا به پاسخ نهایی برسد.
- از الگوریتم Backtracking برای حل مسائلی مانند مسیریابی، جستجو در عمق اول و عمق محدود، حل صریح، ترتیببندی، کولهپشتی و مسائل ترکیبیاتی استفاده میشود.
- الگوریتم Backtracking یک الگوریتم عمومی برای حل مسائل بهینهسازی و جستجو است. این الگوریتم به صورت بازگشتی عمل میکند و راهحلهای ممکن را میآزماید تا به یک راه حل بهینه برسد.
الگوریتم Backtracking چه زمانی مورد استفاده قرار میگیرد؟
مثالی از نحوه استفاده از الگوریتم Backtracking در مسیریابی
الگوریتم Backtracking یک الگوریتم قدرتمند برای حل مسائل مسیریابی است. در اینجا مثالی از استفاده از الگوریتم Backtracking در مسیریابی را مورد بررسی قرار میدهیم. فرض کنید شما یک گراف دارید که شامل چندین شهر است و بین شهرها جادههایی وجود دارد. هدف شما پیدا کردن کوتاهترین مسیر بین دو شهر مشخص است.
مراحل اجرای الگوریتم Backtracking به شرح زیر است:
1. تعریف تابع بازگشتی:
الگوریتم Backtracking از یک تابع بازگشتی به نام "Backtrack" استفاده میکند. این تابع به عنوان ورودی شهر فعلی، شهر مقصد، مسیر فعلی و مسیر کوتاهترین مسیر را دریافت میکند.
2. شرط پایان:
اگر شهر فعلی با شهر مقصد برابر باشد، مسیر فعلی را با مسیر کوتاهترین مسیر مقایسه کرده و در صورت لزوم آن را به روز رسانی میکنیم.
3. حرکت به شهرهای مجاور:
برای هر شهر مجاوری که هنوز در مسیر فعلی حضور ندارد، آن را به مسیر فعلی اضافه کرده و تابع Backtrack را برای آن شهر فراخوانی میکنیم.
4. بازگشت و حذف شهر فعلی:
بعد از اتمام حرکت در همه شهرهای مجاور، شهر فعلی را از مسیر فعلی حذف میکنیم و به شهر قبلی برمیگردیم.
5. اجرای الگوریتم:
برای شروع الگوریتم، تابع Backtrack را با شهر فعلی راهنما، شهر مقصد، مسیر خالی و مسیر کوتاهترین مسیر نامحدود فراخوانی میکنیم.
6. مسیر کوتاهترین مسیر:
پس از پایان اجرای الگوریتم، مسیر کوتاهترین مسیر یافت شده را خروجی میدهیم.
این الگوریتم با بررسی همه مسیرهای ممکن بین دو شهر، مسیر کوتاهترین مسیر را پیدا میکند. با افزایش تعداد شهرها و جادهها، زمان اجرای الگوریتم Backtracking افزایش مییابد. لذا استفاده از الگوریتمهای بهینهتر مانند الگوریتمهای جستجوی مطلع مثل الگوریتم A* نیز پیشنهاد میشود.
الگوریتم Backtracking چه زمانی مورد استفاده قرار میگیرد؟
به طور معمول در ارتباط با مسائل زیر الگوریتم عقبگرد بهترین راهکار را ارائه میکند.
- مسائل مسیریابی: مانند مسیریابی در یک گراف یا یافتن مسیر کوتاهترین بین دو نقطه در یک شبکه جادهای.
- مسائل ترتیببندی (Permutation): مانند یافتن تمام ترتیبهای ممکن برای یک مجموعه از اشیاء.
- مسائل ترکیب (Combination): مانند یافتن تمام ترکیبهای ممکن برای یک مجموعه از اشیاء.
- مسائل تصمیم (Decision): مانند یافتن یک توالی مشخص از اعداد در یک مجموعه.
- مسائل رشتهها (String): مانند یافتن تمام ترتیبهای ممکن برای ترکیب حروف در یک رشته.
- مسائل پر کردن (Filling): مانند پر کردن فضای خالی در یک صفحه با استفاده از اشیاء مختلف.
در این مسائل، الگوریتم Backtracking به عنوان یک روش کامل مورد استفاده قرار میگیرد. این الگوریتم به صورت بازگشتی روی فضای جستجو حرکت میکند و تمام حالتهای ممکن را بررسی میکند تا به جواب نهایی برسد. با این حال، برای مسائلی که فضای جستجو بسیار بزرگ است، الگوریتم Backtracking ممکن است زمان زیادی برای اجرا نیاز داشته باشد و در این موارد ممکن است روشهای بهینهتری مانند الگوریتمهای جستجوی مطلع (Informed Search Algorithms) مورد استفاده قرار گیرند.
ویژگیهای الگوریتم Backtracking
از ویژگیهای شاخص الگوریتم فوق به موارد زیر باید اشاره کرد:
- از بازگشتی بودن و جستجوی نمایش درختی استفاده میکند.
- برای مسائلی کاربرد دارد که راه حلهای متعددی دارند.
- هر بار یک راه حل بالقوه را انتخاب میکند و آن را تا زمانی که به راه حل ممکن برسد یا مسدود شود، دنبال میکند.
- اگر راه بنبست باشد، الگوریتم به عقب بازمیگردد (Backtrack) و راه حل بعدی را امتحان میکند.
- الگوریتم زمانی متوقف میشود که همه راه حلهای ممکن را بررسی کند یا به راه حل بهینه برسد.
- معمولا برای مسائلی مثل مسیریابی، بازیها، و غیره استفاده میشود.
به طور خلاصه، Backtracking یک الگوریتم کارآمد برای یافتن راه حل بهینه در میان تعداد زیادی از راه حلهای ممکن است.
مقایسه میان الگوریتم Backtracking با الگوریتمهای جستجوی مطلع
بله، الگوریتم Backtracking و الگوریتمهای جستجوی مطلع (Informed Search Algorithms) دو دسته متفاوت از الگوریتمها هستند و در برخی جنبهها با یکدیگر متفاوتند. در ادامه، الگوریتم Backtracking را با دو الگوریتم جستجوی مطلع معروف، یعنی الگوریتم DFS (Depth-First Search) و الگوریتم A* مقایسه خواهم کرد:
1. روش جستجو:
- Backtracking: الگوریتم عقبگرد به صورت بازگشتی روی فضای جستجو حرکت میکند و تمام حالتهای ممکن را بررسی میکند تا به جواب نهایی برسد.
- DFS: الگوریتم DFS نیز به صورت بازگشتی عمل میکند، اما در جستجوی عمقی از یک حالت به حالت بعدی پیش میرود تا به جواب برسد.
- A*: الگوریتم A* از استراتژی جستجوی بهینه استفاده میکند و با ترکیب جستجوی به عرض (BFS) و جستجوی به هزینه کمتر (Greedy Best-First Search) عمل میکند. A* از تابع ارزیابی (Heuristic Function) برای تخمین هزینه باقیمانده تا به هدف برسد استفاده میکند.
2. بهینگی:
- Backtracking: الگوریتم عقبگرد برای مسائل که فضای جستجو بزرگی دارند، ممکن است زمان زیادی برای اجرا نیاز داشته باشد و نمیتواند بهینهترین راه حل را پیدا کند.
- DFS: الگوریتم DFS نیز ممکن است در مسائل با فضای جستجو بزرگ، به جواب نهایی نرسد و فضای جستجو را به طور کامل بررسی نکند.
- A*: الگوریتم A* به دلیل استفاده از تابع ارزیابی (Heuristic Function)، میتواند به صورت مطلعتر در فضای جستجو حرکت کند و بهینهترین راه حل را پیدا کند.
3. استفاده در مسائل خاص:
- Backtracking: الگوریتم عقبگرد بیشتر در مسائل مسیریابی، ترتیب بندی، ترکیب، حروفچینی و پرکردن استفاده میشود.
- DFS: الگوریتم DFS برای پیدا کردن مسیرها، درختها، گرافها و مسائلی که نیاز به پیمایش عمقی دارند، کاربرد دارد.
- A*: الگوریتم A* برای مسائل جستجوی مسیر و کوتاهترین مسیر در گرافها و شبکهها، کاربرد دارد.
به طور کلی، الگوریتم عقبگرد در مسائل کامل جستجوی فضای حالات مورد استفاده قرار میگیرد، در حالی که الگوریتمهای جستجوی مطلع مانند DFS و A* برای جستجوی هدف به صورت بهینهتر و با استفاده از اطلاعات بیشتر از فضای جستجو عمل میکنند.
چگونه الگوریتم عقبگرد را در پایتون پیادهسازی کنیم؟
برای پیادهسازی الگوریتم فوق در پایتون، میتوانید از روش بازگشتی استفاده کنید. در اینجا یک نمونه ساده از پیادهسازی الگوریتم عقبگرد در پایتون آورده شده است:
def backtracking(problem, solution):
if is_solution(problem):
process_solution(solution)
else:
candidates = generate_candidates(problem)
for candidate in candidates:
if is_valid(candidate):
make_move(problem, candidate)
add_to_solution(solution, candidate)
backtracking(problem, solution)
remove_from_solution(solution, candidate)
undo_move(problem, candidate)
:در این الگوریتم، توابع زیر به شرح زیر عمل میکنند
- is_solution(problem): یک تابع بولی است که بررسی میکند آیا مسئله به یک حالت پایانی رسیده است یا خیر.
- process_solution(solution): یک تابع است که جواب را پردازش میکند یا آن را چاپ میکند.
- generate_candidates(problem): یک تابع است که لیستی از کاندیدها را برای حالت فعلی مسئله تولید میکند.
- is_valid(candidate): یک تابع بولی است که بررسی میکند آیا یک کاندید معتبر است یا خیر.
- make_move(problem, candidate): یک تابع است که حالت مسئله را با استفاده از یک کاندید تغییر میدهد.
- add_to_solution(solution, candidate): یک تابع است که کاندید را به جواب (solution) اضافه میکند.
- remove_from_solution(solution, candidate): یک تابع است که کاندید را از جواب (solution) حذف میکند.
- undo_move(problem, candidate): یک تابع است که تغییراتی که در حالت مسئله با استفاده از کاندید انجام شده است را برگردانده و حالت مسئله را به حالت قبلی بازمیگرداند.
شما باید این توابع را براساس نیازهای خاص مسئله خود پیادهسازی کنید. همچنین، میتوانید متغیرهای دیگری مانند شمارندهها و متغیرهای وضعیت برای بهبود عملکرد الگوریتم Backtracking در نظر بگیرید. توجه داشته باشید که الگوریتم Backtracking ممکن است برای مسائلی با فضای جستجو بزرگ و پیچیده، زمان اجرای طولانی داشته باشد. در این موارد، ممکن است نیاز به بهینهسازیهایی مانند پروش کردن بخشی از فضای جستجو و یا استفاده از الگوریتمهای بهینهتر باشد.
یک مثال کاربردی دیگر از الگوریتم عقبگرد در پایتون
برای درک بهتر موضوع اجازه دهید به مثال دیگری اشاره داشته باشیم. در این مثال قصد داریم از الگوریتم عقبگرد برای یک مسئله مسیریابی بازگشتی (Recursive Pathfinding) استفاده کنیم. در این مسئله، هدف ما پیدا کردن مسیری است که از یک نقطه شروع به یک نقطه پایانی برسیم، با این تفاوت که مجاز است به سمتهای مختلف حرکت کنیم (با گامهای عمودی یا افقی) و میتوانیم از برخی خانهها عبور کنیم و برخی خانهها را ببندیم. در زیر، یک نمونه ساده از پیادهسازی الگوریتم عقبگرد برای مسئله مسیریابی بازگشتی در پایتون آمده است:
def recursive_pathfinding(grid, start, end, path):
i, j = start
if start == end:
path.append(start)
return True
if is_valid_move(grid, start):
path.append(start)
grid[i][j] = "#" # برای علامتگذاری خانهای که قبلاً رفتهایم
# حرکت به سمت بالا
if recursive_pathfinding(grid, (i-1, j), end, path):
return True
# حرکت به سمت پایین
if recursive_pathfinding(grid, (i+1, j), end, path):
return True
# حرکت به سمت چپ
if recursive_pathfinding(grid, (i, j-1), end, path):
return True
# حرکت به سمت راست
if recursive_pathfinding(grid, (i, j+1), end, path):
return True
# خروج از خانه و برگشت به حالت اولیه
path.pop()
grid[i][j] = "."
return False
# مثال استفاده
grid = [
[".", ".", ".", ".", "#"],
["#", "#", ".", "#", "#"],
[".", ".", ".", ".", "#"],
["#", "#", "#", "#", "."],
[".", ".", ".", ".", "."]
]
start = (0, 0)
end = (4, 4)
path = []
if recursive_pathfinding(grid, start, end, path):
print("مسیر پیدا شد:")
for point in path:
print(point)
else:
print("مسیری پیدا نشد.")
در این مثال، ما یک شبکه ۵×۵ به عنوان نمایشی از محیط مسئله داریم. خانههای `.` به معنی خانههای قابل عبور و خانههای `#` به معنی خانههای بسته است. ما از تابع recursive_pathfinding برای پیدا کردن مسیر استفاده میکنیم. این تابع به صورت بازگشتی حرکت میکند و در هر مرحله، خانههای مجاز را بررسی میکند و در صورت معتبر بودن، به سمت آن خانه حرکت میکند. در نهایت، مسیر پیدا شده یا عدم وجود مسیر را چاپ میکنیم.
لازم به توضیح است که این یک نمونه ساده از کاربرد الگوریتم عقبگرد در پایتون برای حل مسئله N-Queen یا همان مسئله معروف وزیر در شطرنج است. در این مسئله، هدف ما قرار دادن N وزیر در صفحه شطرنج به نحوی است که هیچ دو وزیری یکدیگر را تهدید نکنند، به این معنی که هیچ دو وزیر در یک سطر، ستون یا قطری واحد قرار نگیرند.
در زیر، یک نمونه کد پایتون برای حل مسئله N-Queen با استفاده از الگوریتم Backtracking آورده شده است:
def is_valid(board, row, col):
# بررسی ستونها در سطر فعلی
for i in range(col):
if board[row][i] == 1:
return False
# بررسی قطر بالا و راست
i, j = row, col
while i >= 0 and j >= 0:
if board[i][j] == 1:
return False
i -= 1
j -= 1
# بررسی قطر پایین و راست
i, j = row, col
while i < len(board) and j >= 0:
if board[i][j] == 1:
return False
i += 1
j -= 1
return True
def solve_n_queen(board, col):
if col >= len(board):
return True
for i in range(len(board)):
if is_valid(board, i, col):
board[i][col] = 1
if solve_n_queen(board, col + 1):
return True
board[i][col] = 0
return False
def print_board(board):
for row in board:
print(row)
def solve_n_queen_problem(n):
board = [[0] * n for _ in range(n)]
if solve_n_queen(board, 0):
print(f"یک راه حل برای {n}-Queen:")
print_board(board)
else:
print(f"هیچ راه حلی برای {n}-Queen وجود ندارد.")
# مثال استفاده
solve_n_queen_problem(4)
در این مثال، تابع is_valid برای بررسی صحت قرارگیری وزیر در یک خانه خاص استفاده میشود. تابع solve_n_queen به صورت بازگشتی وزیرها را در ستونهای مختلف قرار میدهد و با استفاده از تابع is_valid بررسی میکند که آیا وضعیت فعلی معتبر است یا خیر. در صورتی که راه حلی پیدا شود، تابع print_board برای چاپ صفحه شطرنج با وزیرهای قرارداده شده استفاده میشود.
در این مثال، برای حل مسئله 4-Queen، راه حل به شرح زیر خواهد بود:
[0, 1, 0, 0]
[0, 0, 0, 1]
[1, 0, 0, 0]
[0, 0, 1, 0]
ماهنامه شبکه را از کجا تهیه کنیم؟
ماهنامه شبکه را میتوانید از کتابخانههای عمومی سراسر کشور و نیز از دکههای روزنامهفروشی تهیه نمائید.
ثبت اشتراک نسخه کاغذی ماهنامه شبکه
ثبت اشتراک نسخه آنلاین
کتاب الکترونیک +Network راهنمای شبکهها
- برای دانلود تنها کتاب کامل ترجمه فارسی +Network اینجا کلیک کنید.
کتاب الکترونیک دوره مقدماتی آموزش پایتون
- اگر قصد یادگیری برنامهنویسی را دارید ولی هیچ پیشزمینهای ندارید اینجا کلیک کنید.
























نظر شما چیست؟